Cycles

Chapters > Graphs

Do you ever heard of the "Chicken and Egg" dilemma? It, pictured on the right, is there to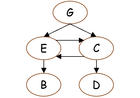

remind us that cycles in a directed graph are illusions because every cyclic directed graph has an acyclic skeleton.

But how do we come to this conclusion? Let us start from the beginning.

Pseudo Cycles Real Cycles

Initially, only node G, the genesis, exists. Next is the insertion of an egg, E, or of a chicken, C, depending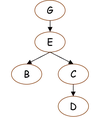

on which one we observe first. Assume that we observe first an egg. The edge (G,E) is inserted into the graph. An egg can either become a chicken C, or it can get broken, B. We indicate both possibilities as edges (E,C) and (E,B), respectively. A chicken may die, D, indicated with the edge(C,D).

Another transition that we can observe is the chicken laying an edge. The question is whether it is the same egg we observed previously. The answer is "for sure not". But would we not mean "yes", if we insert an edge (C,E)? To avoid a confusion, we should say what we mean "for sure not, it is a new egg. But this egg has to follow all paths starting at an egg as any other egg". This is the point where the start of a cycle meets the end of another.

The definition of a back-edge comes for rescue.

An edge is called a back-edge if the head of the edge is connected to its tail.

We insert a special edge (C,@E) where node @E is meant to be a proxy of the node E. The proxy is unique, does not have a successor, and should be rather considered as a pointer to the node it is the proxy of. Besides that, only the algorithm is allowed to introduce an edge with a proxy as its head.

In case chicken has been observed first, we would have a similar picture of the graph after the

cycle has been broken. The edge with the proxy of node C as its head, (E,@C), is the cycle breaker.

A question remains unanswered if we do not wait until we make an observation, though:

What are the possible paths starting at the Genesis?

The next section discusses how to achieve an answer, and why we call that there are two distinct types of cycles.

The ultimate target of every path through a graph is a node with no successor, except for those paths which are cyclic, where the last node is the head of a back-edge, also a so-called proxy. Therefore, we can classify each path on a graph either as a cyclic or acyclic one. As a consequence, cyclic paths which share the same cycle-head build an isolated bundle.

Let us consider the paths starting at Genesis; [G, E, B], [G, E, C, D], [G, E, C, @E], and [G, C, D], [G, C, E, B], [G, C, E, @C].

A closer look at the cycling paths shows another reality, though. The path [(G,E), (E,C), (C,E)] could end with the edge (E,B), which causes the path to be completed without cycling. Similarly, the path [(G,C), (C,E), (E,C)] could end, if the chicken dies.

We call the (partial) path [G, E, C, @E] a "Pseudo Cycle" because the path is completed with a reference to a node.

The "Real Cycle" is [(G,E), (E,C), (C,E), @(E,C)].

A real cycle is completed with a reference to an edge within the path, but not with a reference to a node.

We can argue similarly if chicken is observed first.

Now we can have an overview of all paths through the chicken-and-egg dilemma:

[(G,E), (E,B)]
[(G,E), (E,C), (C,E), (E,B)]
[(G,E), (E,C), (C,E), @(E,C)]
[(G,E), (E,C), (C,D)] and

[(G,C), (C,D)]
[(G,C), (C,E), (E,C), (C,D)]
[(G,C), (C,E), (E,C), @(C,E)]
[(G,C), (C,E), (E,B)]

If a model level analysis of cycles is required, an edge-oriented representation of the graph should be chosen.

Who was there first, a chicken or an egg, is not a dilemma. It can be any of them, depending on one's observation. Then the life takes its course with unique, although cyclic, paths.

Once we are out of the cycle, there is no way to enter into the cycle again. Even going back to genesis does not allow us to reenter the cycle. It will be a new cycle.