Lists
Chapters > Graphs
Structure
In the previous chapter, we built a path and used the rule of transitivity to deduce that Joan is older than Melanie. If the path built is the only one possible through the graph, then the graph is said to have a list-structure, or it is a list. The conditions to recognize a list-structured graph are:
- Exactly one node has no predecessor (the Source)
- Exactly one node has no successor (the Sink)
- All other nodes have exactly one predecessor, and one successor
The graph can be shown as
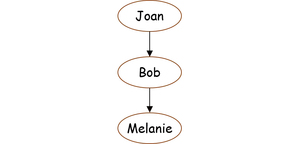

where node Joan is the Source and node Melanie is the Sink.
Topology
If a graph is of list-structure, only one path through the graph is possible. This path corresponds to the spanning list of the nodes of the graph. Here [Joan, Bob, Melanie].
If the graph's structure is a list, from two nodes the one on the left in the spanning list of the graph is related to the one on the right in the direction of the relation.
According to this rule, the list [Joan, Bob, Melanie] can be decoded as a set of edges {(Joan,Bob), (Joan, Melanie), (Bob,Melanie)}, and is equivalent to the set of edges of the respective graph.
The set of edges of a list structured directed graph and its spanning list are equivalent.

