Trees
Chapters > Graphs
Structure
Let us introduce a new node (Joan,Neil). The graph's picture becomes;
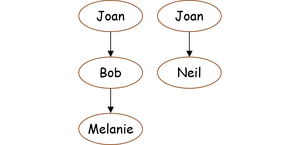
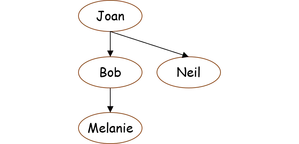
It is obvious that node Joan is a duplicate. This is not conforming to the principle that identical nodes of the graph can only exist once. A correct picture of the graph has to be
If nodes of a graph comply with the following conditions, the graph is said to have a tree-structure, or it is a tree:
- Exactly one node has no predecessor (the Source)
- A distinguished node Sink succeeds all nodes which does not have a successor
- Exactly one node has no successor (the Sink)
- All other nodes have exactly one predecessor, and at least one successor
- Nodes whose predecessor is the same node are called siblings
- Node A can reach node B, if there exists a path from node A to node B. Node B then is called to be reachable from node A
- Two nodes are connected if one can reach the other
Topology - Process
The procedure to obtain a spanning list of a tree leans on the well known depth-first-search algorithm:- Start with the Source as current node
- Proceed with the next (from left to right) node of the successors of the current node, starting with the first
- If there is no more successor to be discovered,
- Proceed along the predecessors (that is, in the reverse direction of the relation, upwards in the picture) of the current node until a predecessor with a successor still to be discovered is found, and make it the current node. The current node thrives a new branch.
- If no predecessor can be found, stop the process
- Append current node to the spanning list
- Resume at (2)
Applying the procedure yields [Joan, Bob, Melanie, Neil].
As we can easily verify, the rule we stated previously does not hold. The spanning list claims erroneously that Bob, and Melanie are older than Neil. We can verify the misleading claims, and let them be either confirmed or denied by a second spanning list of the graph.
To generate the second spanning list we use the same procedure, but process the successors of the nodes in the reverse order, i.e. from right to left.
- Start with the Source as current node
- Proceed with the next (from right to left) node of the successors of the current node, starting with the last
- If there is no more successor to be discovered,
- Proceed along the predecessors of the current node until a predecessor with a successor still to be discovered is found, and make it the current node. The current node thrives a new branch.
- If no predecessor can be found, stop the process
- Append current node to the spanning list
- Resume at (2)
If the graph's structure is a tree, from two nodes the one on the left in both of the spanning lists of the graph is related to the one on the right in the direction of the relation.
Topology - Proof
Trees have an interesting feature. Because every node has a unique predecessor, all descendants of a node are discovered during the depth-first-search process before the node is exhausted, no matter in which direction we carry the search (see steps 3.a. of the procedures mentioned in the previous section). Of course, a node cannot reach the node next to it in the spanning list if it is not its descendant. For our example, the spanning lists are; left-to-right [Joan, Bob, Melanie, Neil], and right-to-left [Joan, Neil, Bob, Melanie].
Confirming a connection
Because all nodes are inserted to the right of their predecessors in the spanning lists, confirmation of a connection is always granted.
Denying a connection
If we traverse a tree in opposite directions, nodes which are discovered earlier in the first case will be discovered later in the second case, except descendants which are always discovered later than their predecessor. Consequently, nodes which are not connected are positioned oppositely in two tightly coupled spanning lists, while their descendants kept to the right of them (see steps 3 and 4 of the procedures mentioned in the previous section). Therefore, a claimed connection by one of the spanning lists is denied by the other if the nodes are not in an ascendant/descendant relationship to each other.
The pair of spanning lists above confirms the claimed relations by the left-to-right spanning list (Joan,Bob), (Joan,Melanie), (Joan.Neil), (Bob,Melanie), but denies (Bob,Neil), and (Melanie,Neil).
We could have used the right-to-left spanning list as the claimer and the left-right spanning list as the verifier because they are a tightly coupled pair, and exchangeable in their roles.
Using the spanning lists we can only generate the edges (Joan,Bob), (Joan,Melanie), (Joan,Neil), and (Bob,Melanie), they encode all possible paths through the respective graph. These are [Joan, Bob, Melanie], and [Joan, Neil].
Later on, when we discuss the details of the algorithm, we will show how spanning lists of a tree structured graph can be maintained incrementally, and in constant time per edge insertion.