Transitivity and Paths
Chapters > Graphs
Now our graph contains two edges, (Joan,Bob) and (Bob,Melanie). Do we have sufficient information to complete our task? The answer is: "Yes".
To obtain a solution, we apply the rule of transitivity
Given two edges (a, b) and (b,c), the transitivity rule implies that (a,c) is also an edge
and deduce that (Joan,Melanie) is also an edge because (Joan,Bob), and (Bob,Melanie) are edges, meaning Joan is older than Melanie, or Melanie is younger than Joan (edges are bidirectional). We add the edge (Joan,Melanie) to the graph. Task accomplished.
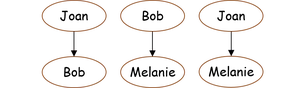
In general, transitivity is a recipe to apply deduction on chains (paths) of edges. To build a path
- Start with an edge
- If the tail of the next edge is the same as the head of the last edge on the path, add the edge to the end of the path
- Proceed with the next edge, until all edges of the graph are exhausted
Starting with the node (Joan,Bob) and applying this procedure to our graph, we obtain the path [(Joan,Bob), (Bob,Melanie)], or [Joan, Bob, Melanie] in short.
Due to transitivity, all nodes on a path are related to each other, even if they are not adjacent. Because Joan and Melanie are on the path, we can decide that they are related (connected), and creating an edge (Joan,Melanie) is legitimate.

