Domination in Graphs
Chapters > Graphs
If node A is on all paths targeting node B, then node A is said to be a pre-dominator of node B. Every node has at least one pre-dominator.
Every path in a graph starts with the Source, and therefore it is the pre-dominator of all nodes. There is no limit on the number of pre-dominators. If there is more than one node which dominates a node, the nearest to the node is called its immediate pre-dominator.
A pre-dominator is the entry of a sub-graph which, like a check-point, controls the flow into the sub-graph.
If node B is on all paths starting at node A, then node B is said to be a post-dominator of node A. Every node has at least one post-dominator.
Like every path starts with the Source, every path ends with the Sink or a cycle-head, and therefore, every node has a post-dominator. There is no limit on the number of post-dominators. If a node has more than one post-dominator, the nearest to the node is called its immediate post-dominator.
A post-dominator is the exit of a sub-graph which, like a check-point, controls the flow out-off the sub-graph.
Dominators play a decisive role in the graph's decomposition, and determination of its structure.
The control-flow diagram of a snippet of a computer program is used  to demonstrate the domination notion in directed graphs.
to demonstrate the domination notion in directed graphs.
 to demonstrate the domination notion in directed graphs.
to demonstrate the domination notion in directed graphs.The idea of pre-domination is to determine the last node, where all external influences before a node gets control comes to a still stand. For the post-domination, we can say that it is the first check-point where all paths leaving a node join a single node.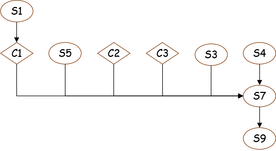 The post-dominators build a tree as well (shown on the left). The idea is to stop the flow at a single node, where all paths containing a particular node join. In the sample except C1 and S9, S7 is the only post-dominator.
The post-dominators build a tree as well (shown on the left). The idea is to stop the flow at a single node, where all paths containing a particular node join. In the sample except C1 and S9, S7 is the only post-dominator.
The pre-dominators in the sample graph build a tree. S1, the source, dominates all statements. C1 is the pre-dominator of S7 because from S1 and C1, C1 is nearer to S7. S7 is  the node which is common to all paths reaching S9. It blocks, or provides an opportunity to freeze, before the flow reaches S9.
the node which is common to all paths reaching S9. It blocks, or provides an opportunity to freeze, before the flow reaches S9.
 the node which is common to all paths reaching S9. It blocks, or provides an opportunity to freeze, before the flow reaches S9.
the node which is common to all paths reaching S9. It blocks, or provides an opportunity to freeze, before the flow reaches S9.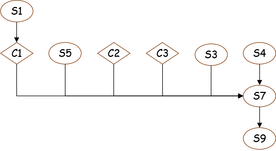 The post-dominators build a tree as well (shown on the left). The idea is to stop the flow at a single node, where all paths containing a particular node join. In the sample except C1 and S9, S7 is the only post-dominator.
The post-dominators build a tree as well (shown on the left). The idea is to stop the flow at a single node, where all paths containing a particular node join. In the sample except C1 and S9, S7 is the only post-dominator.Dominators determine the structure of a directed graph, as we will see in the next section.
How is a graph organized, or what is the structure of a graph? To answer these questions, we have to refer to the definition of what a graph is. Does any subset of the graph's content, the set of edges of it, comply with the definition? If yes, then the particular subset is a sub-graph.
Once all the sub-graphs are determined, decomposition of the graph is completed, and we look forward to exploring the graph's structure. This is about how sub-graphs are related to each other. A relation is either "nested", meaning a sub-graph contains the other completely, or two sub-graphs are in sequence.
This may sound like a tedious task. On the other hand, pre- and post-domination graphs contain all  the information we need.
the information we need.
 the information we need.
the information we need.- Every pre-dominator is a potential Source for a sub-graph which contains all the nodes it dominates.
- Every post-dominator is a potential Sink for a sub-graph which contains all the nodes it dominates.
- If a pre-dominator dominates its post-dominator, they are an Entry-Exit pair which define the boundaries of a sub-graph.
This is an agreed upon definition of a sub-graph in the literature, although it is an overkill. If we relax the condition how an Entry-Exit pair is built, we can achieve a composition of the graph which is of a better granularity.
graph which is of a better granularity.
 graph which is of a better granularity.
graph which is of a better granularity.- Every pre-dominator is a potential Entry.
- If a pre-dominator dominates all nodes it can reach, up to but not including its post-dominator, the pre-dominator and its post-dominator constitute an Entry-Target sub-graph.
- The set of nodes an Entry dominates, excluding its Target, is called the Body of the sub-graph.
Fortunately dominators of a graph can be computed while an edge is processed. The time required by the computation is linear with respect to the depth of the dominator trees at the time of edge insertion.

